Lagrangian Mechanics: Difference between revisions
NickPGSmith (talk | contribs) Tag: Reverted |
NickPGSmith (talk | contribs) Tag: Manual revert |
||
| Line 4: | Line 4: | ||
The [http://en.wikipedia.org/wiki/Lagrangian Lagragian] is defined to be: | The [http://en.wikipedia.org/wiki/Lagrangian Lagragian] is defined to be: | ||
:<math>\mathcal{L}(q_i, \dot{q}_i) = T(q_i, \dot{q}_i) - U(q_i, \dot{q}_i)</math> | :<math>\mathcal{L}(q_i, \dot{q}_i) = T(q_i, \dot{q}_i) - U(q_i, \dot{q}_i)</math> | ||
Revision as of 04:37, 9 May 2024
Principle of Stationary Action
Consider a physical system described by the generalised coordinates and matching velocities
The Lagragian is defined to be:
where T is the Kinetic Energy and U is the Potential Energy. Typically, the Lagrangian is not a conserved quantity.
The Action is defined as:
Hamilton's Principle of Stationary Action (sometimes referred to as "Least Action") states that a physical system evolves in time such that the Action is stationary functional of the generalised coordinates:
It can be shown that this leads to the Euler-Lagrange condition:
where is the Generalised Force and is the Momentum Canonically Conjugate to .
Examples
Translational Symmetry and Linear Momentum
Consider the system of two particles constrained to move in a line, at positions and , with masses and . Their potential energy is only a function of the distance between them . That is, there is translational (continuous) symmetry in the system.
The Lagrangian is:
- .
The Euler-Lagrange condition leads to:
- and
which is
- and
where is the linear momentum.
Now, , so
This states that the total linear momentum is constant, or momentum is conservered. Thus, we have shown that from the original translational symmetry in space of the system, one can derive conservation of linear momentum.
Rotational Symmetry and Angular Momentum
Consider a particle of mass moving within a Central Force, where the potential energy depends only on the distace from the origin: . The radial and angular components of velocity are given by: and .
The Lagrangian is:
- .
The Euler-Lagrange condition for r and is:
- and
which gives:
- , noting that the angular momentum of the system is .
The first equation shows that the radial component of momentum is composed of a positive (repulsive) force that is not dependent on the potential energy, but is due to the rotation. This is the origin of the Centrifugal Force. The second equation states that the rate of change of angular momentum is zero. That is, following from the rotational invariance of the system, we have derived conservation of angular momentum.
We may also write the force on the particle in terms of , which shows the centrifugal component depends inversely on :
- .
Double Pendulum
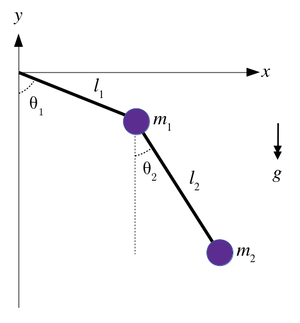
Consider the double pendulum consisting of two masses connected by to rigid massless rods, to a fixed point of rotation at the origin and each other in a frictionless manner, constrained in the vertical plane, as shown above.
The kinetic energy is given by:
where
after substitution and use of a standard trig identity, we find:
The potential energy is given by:
The Lagrangian is thus:
Using the Euler-Lagrange condition for :
thus:
Using the Euler-Lagrange condition for :
thus:
Now we can form the two equations of motion:
Hence determine how the angular acceleration changes:
